A Cebisev-szűrők nevét „Pafnufy Chebyshev” -nek nevezik, mert matematikai jellemzői csak az ő nevéből származnak. A Chebyshev szűrők nem más, mint analóg vagy digitális szűrők. Ezeknek a szűrőknek van egy meredekebb roll-off és 1-es típusú szűrője (több áthidalási sáv hullámzása) vagy 2-es típusú szűrője (leállítási sáv hullámzása), mint Butterworth szűrők . Ennek a szűrőnek az a tulajdonsága, hogy csökkenti a tényleges és az idealizált szűrő jellemzői közötti hibát. Mivel, a pass sáv hullámzása ebben a szűrőben.
Chebyshev Filter
A Chebyshev-szűrőket az egyik sáv különböző frekvenciáira használják. Nem felelnek meg az ablak-mosogató szűrő teljesítményének, és sok alkalmazásra alkalmasak. A Chebyshev szűrő fő jellemzője a sebességük, általában gyorsabb, mint az ablakos-sinc. Mivel ezeket a szűrőket rekurzióval hajtják végre, nem pedig konvolúcióval. A Chebyshev és a Windowed-Sinc szűrők megtervezése egy Z-transzformációnak nevezett matematikai technikától függ.

Chebyshev Filter
A Csebisev-szűrők típusai
A csebisev szűrőket két típusba sorolják, nevezetesen az I. típusú és a II. Típusú csebisev szűrőket.
I. típusú Chebyshev szűrők
Ez a típusú szűrő a Chebyshev szűrő alapvető típusa. Az amplitúdó vagy az erősítési válasz az LPF (aluláteresztő szűrő) n-edik sorrendjének szögfüggvénye egyenlő a Hn (jw) átviteli függvény teljes értékével
Gn (w) = | Hn (jω) | = 1√ (1 + ϵ2Tn2 () ω / ωo)
Hol, ε = hullámtényező
ωo = vágási frekvencia
Tn = az n-edik rendű Chebyshev-polinom
A pass band egyenlő teljesítményt mutat. Ebben a sávban a szűrő -1 és 1 között változik, így a szűrő erősítése max G = 1 és min között G = 1 / √ (1 + ε2) között változik. A határértéknél az erősítés értéke 1 / √ (1 + ε2), és a frekvencia növekedésével továbbra is a stop sávba esik. A szűrő viselkedése az alábbiakban látható. A -3dB-os határértéket általában nem alkalmazzák Chebyshev szűrőkre.

I. típusú Chebyshev-szűrő
A szűrő sorrendje hasonló a nemhez. a Chebyshev-szűrőhöz szükséges reaktív komponensek felhasználásával analóg eszközök. A hullámzás dB-ben 20log10 √ (1 + ε2). Annak érdekében, hogy a 3db hullámzásának amplitúdója az ε = 1 eredményéből származik. Még meredekebb lefutás található, ha a hullámzás megengedett a stop sávban, lehetővé téve a 0-okat a jw tengelyen a komplex síkban. Pedig ez a hatás a stop sávban kevesebb elnyomással jár. A hatást Cauer- vagy elliptikus szűrőnek hívják.
Az I. típusú Chebyshev-szűrő pólusai és nullai
Az 1. típusú Chebyshev-szűrő pólusait és nullait az alábbiakban tárgyaljuk. A Csebisev-szűrő pólusait a szűrő erősítésével lehet meghatározni.
 -js = cos (θ) és a szűrő trigonometrikus meghatározása így írható fel
-js = cos (θ) és a szűrő trigonometrikus meghatározása így írható fel

Itt θ megoldható

Ahol az ív koszinusz függvény sok értéke egyértelművé vált az m számindex használatával. Ekkor a Csebisev-nyereség-pólusok funkciói
 A hiperbolikus és a trigonometrikus függvények tulajdonságait felhasználva ezt a következő formában írhatjuk fel
A hiperbolikus és a trigonometrikus függvények tulajdonságait felhasználva ezt a következő formában írhatjuk fel
“4-16 dekóder ”

A fenti egyenlet megalkotja a G nyereség pólusait. Minden egyes pólushoz tartozik egy komplex konjugátum, és minden egyes konjugátumpárhoz még két negatív tartozik. A TF-nek stabilnak kell lennie. Az átviteli függvényt (TF) a

II. Típusú Chebyshev-szűrő
A II Chebyshev szűrő inverz szűrő néven is ismert, ez a típusú szűrő ritkábban fordul elő. Mert nem gördül le, és szüksége van rá különféle alkatrészek . A hágósávban nincs hullámossága, de a leállítási sávban ugyanolyan. A II. Típusú Chebyshev szűrő erősítése
 A stop sávban a Chebyshev-polinom -1 és 1 között változik, így a „G” erősítés nulla és
A stop sávban a Chebyshev-polinom -1 és 1 között változik, így a „G” erősítés nulla és

II. Típusú Chebyshev-szűrő
 A legkisebb frekvencia, amellyel ezt a max-ot eléri, a határérték
A legkisebb frekvencia, amellyel ezt a max-ot eléri, a határérték

5 dB leállási sáv csillapítás esetén az ε értéke 0,6801, a 10dB leállítási sáv csillapítása esetén az ε értéke 0,3333. A vágási frekvencia f0 = ω0 / 2π0, és az fH 3dB frekvencia a következőképpen származik
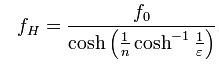 A II. Típusú Chebyshev-szűrő pólusai és nullai
A II. Típusú Chebyshev-szűrő pólusai és nullai
Tegyük fel, hogy a vágási frekvencia egyenlő 1-vel, a szűrő pólusai az erősítés nevezőjének nullái
 A II. Típusú szűrő erősítésének pólusai ellentétesek az I. típusú Chebyshev szűrő pólusaival
A II. Típusú szűrő erősítésének pólusai ellentétesek az I. típusú Chebyshev szűrő pólusaival

Itt a fenti egyenletben m = 1, 2,…, n. A II-es típusú szűrő nullái az erősítés számlálójának nullái

A II. Típusú Chebyshev-szűrő nullái ellentétesek a Chebyshev-polinom nulláival.
 Itt m = 1,2,3, ……… n
Itt m = 1,2,3, ……… n
Bal oldali félsík használatával a TF megkapja az erősítés függvényét, és hasonló nullákkal rendelkezik, amelyek egyszeresek, nem pedig kettős nullák.
Így itt minden a Chebyshev szűrőről, a Chebyshev szűrő típusairól, a Chebyshev szűrő pólusairól és nulláiról, valamint az átviteli függvény kiszámításáról szól. Reméljük, hogy jobban megértette ezt a koncepciót, valamint bármilyen kérdést felvet a témával kapcsolatban elektronikai projektek , kérjük, adja meg visszajelzését az alábbi megjegyzés részben kommentálva. Itt van egy kérdés az Ön számára, mik a Chebyshev szűrők alkalmazásai?
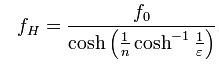 A II. Típusú Chebyshev-szűrő pólusai és nullai
A II. Típusú Chebyshev-szűrő pólusai és nullai