Az egyszerű harmonikus mozgást báró Jean Baptiste, Joseph Fourier francia matematikus találta ki 1822-ben. Edwin Armstrong (1890. december 18. – 1954. február 1.) 1992-ben kísérleteiben észlelte az oszcillációkat, Alexander Meissner (1883. szeptember 14. – 1958. oszcillátorok A harmonikus kifejezés latin szó. Ez a cikk a harmonikus oszcillátor áttekintését tárgyalja, amely tartalmazza annak definícióját, típusát és alkalmazásait.

Mi az a harmonikus oszcillátor?

A harmonikus oszcillátort olyan mozgásként definiálják, amelyben az erő az egyensúlyi ponttól közvetlenül arányos a részecskével, és szinuszos hullám alakban produkálja a kimenetet. A harmonikát okozó erő mozgás matematikailag kifejezhető

F = -Kx

Hol,

F = Helyreállító erő

K = rugóállandó

X = Távolság az egyensúlytól

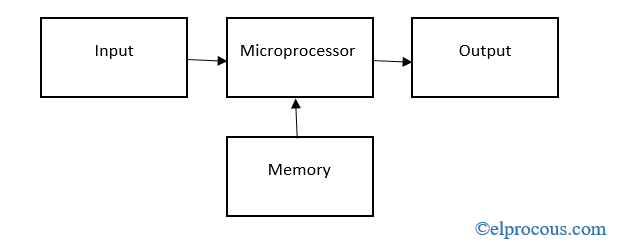
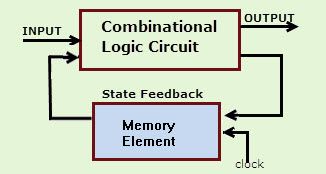
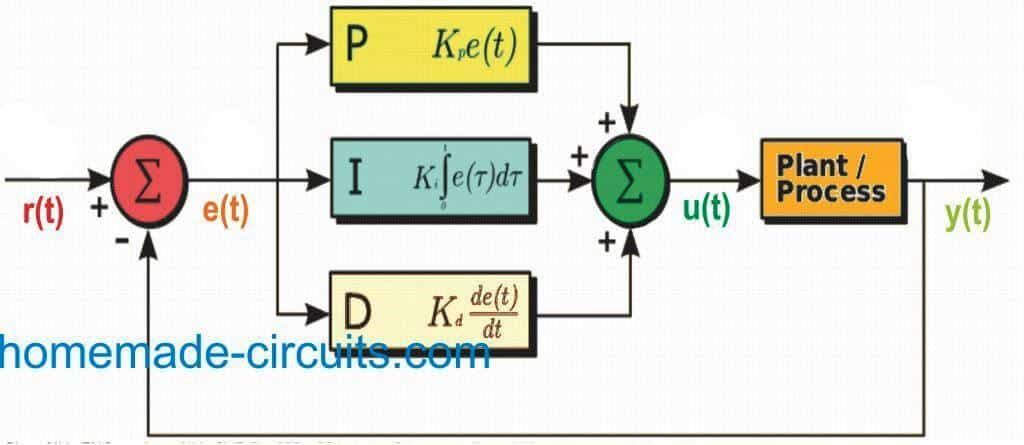
harmonikus oszcillátor blokkdiagramja

A harmonikus mozgásnak van egy olyan pontja, amelyben a rendszer rezeg, és az az erő, amely újra és újra hozza a tömeget ugyanabban a pontban, ahonnan indul, az erőt helyreállító erőnek, a pontot pedig egyensúlyi pontnak vagy átlagos helyzetnek nevezzük. Ezt az oszcillátort más néven a lineáris harmonikus oszcillátor . Az energia aktívból áramlik alkatrészek passzív alkatrészekre az oszcillátorban.

Blokk diagramm

A a harmonikus oszcillátor blokkvázlata tartalmaz egy erősítő és egy visszacsatolási hálózat. Az erősítőt arra használják, hogy felerősítsék a jeleket, és hogy az erősített jeleket egy visszacsatoló hálózaton keresztül továbbítsák és kimenetet generálják. Ahol Vi a bemeneti feszültség, Vo a kimeneti feszültség és Vf a visszacsatolási feszültség.

Példa

Szentmise egy tavaszon: A rugó helyreállító erőt biztosít, amely felgyorsítja a tömeget, és a helyreállító erő kifejeződik

F = ma

Ahol ’m’ a tömeg, az a pedig gyorsulás.

“akadály elkerülése robot segítségével ultrahangos arduino érzékelő ”

tömeg a tavaszon

A rugó tömegből (m) és erőből (F) áll. Amikor az erő húzza a tömeget egy x = 0 pontban, és csak x-től függ - a tömeg helyzetétől és a rugóállandót k betűvel ábrázoljuk.

A harmonikus oszcillátor típusai

Ennek az oszcillátornak a típusai főleg a következőket tartalmazzák.

Kényszerített harmonikus oszcillátor

Amikor külső erőt alkalmazunk a rendszer mozgására, akkor azt mondjuk, hogy a mozgás kényszerített harmonikus oszcillátor.

Csillapított harmonikus oszcillátor

Ezt az oszcillátort úgy definiáljuk, hogy amikor külső erőt fejtünk ki a rendszerre, akkor az oszcillátor mozgása csökken, és mozgását csillapított harmonikus mozgásnak mondják. Háromféle csillapított harmonikus oszcillátor létezik

csillapító-hullámformák

Over Damped

Amikor a rendszer lassan halad az egyensúlyi pont felé, akkor azt mondják, hogy egy túlcsillapított harmonikus oszcillátor.

Csillapított alatt

Amikor a rendszer gyorsan halad az egyensúlyi pont felé, akkor azt mondják, hogy egy túlcsillapított harmonikus oszcillátor.

Kritikus csillapított

Amikor a rendszer a lehető leggyorsabban mozog anélkül, hogy az egyensúlyi pont körül ingadozna, akkor azt túlzottan csillapított harmonikus oszcillátornak mondják.

Kvantum

Max Born, Werner Heisenberg és Wolfgang Pauli találta ki a „Gottingeni Egyetemen”. A kvantum szó a latin szó, a kvantum jelentése pedig kis mennyiségű energia.

Nulla pont energia

A nulla pont energiája alapállapotú energia néven is ismert. Akkor definiálják, amikor az alapállapotú energia mindig nagyobb, mint nulla, és ezt a koncepciót Max Planck fedezi fel Németországban, és az 1990-ben kidolgozott képletet.

A csillapított egyszerű harmonikus oszcillátoregyenlet átlagos energiája

Kétféle energia létezik: kinetikus energia és potenciális energia. A kinetikus energia és a potenciális energia összege megegyezik az összes energiával.

E = K + U ………………. Eq (1)

Ahol E = teljes energia

K = kinetikus energia

U = potenciális energia

Ahol k = k = 1/2 mv^két………… egyenérték (2)

U = 1/2 kx^két………… egyenérték (3)

oszcillációs ciklus - átlagos értékek

A mozgási és a potenciális energia oszcillációs ciklusonkénti átlagos értéke megegyezik

Hol v^két= v^két(NAK NEK^két-x^két) ……. egyenérték (4)

Az (e) (2) és (3) eq helyettesítse az (4) egyenletet

k = 1/2 m [tömeg^két(NAK NEK^két-x^két)]

= 1/2 m [Aw cos (wt + ø₀)]^két……. egyenérték (5)

U = 1/2 kx^két

= 1/2 k [A bűn (wt + ø₀)]^két……. egyenérték (6)

Az eq (5) és az eq (6) helyettesítése az (1) egyenletben megkapja a teljes energiaértéket

E = 1/2 m [tömeg^két(NAK NEK^két-x^két)] + 1/2 kx^két

= 1/2 m sz^két-1/2 m sz^kétNAK NEK^két+ 1/2 kx^két

= 1/2 m sz^kétNAK NEK^két+1/2 x^két(K-mw^két) ……. egyenérték (7)

Hol mw^két= K , helyettesítse ezt az értéket egyenértékben (7)

E = 1/2 K A^két- 1/2 Kx^két+ 1/2 x^két= 1/2 K A^két

Teljes energia (E) = 1/2 K A^két

Az átlagos időtartamok egy időtartamra kifejezve

NAK NEK_Átl= U_Átl= 1/2 (1/2 K A^két)

Harmonikus oszcillátor hullám funkció

A hamiltoni operátort kinetikus energia és potenciális energia összegeként fejezzük ki, és ezt fejezzük ki

ђ (Q) = T + V ……………… .eq (1)

Ahol ђ = hamitoni operátor

T = kinetikus energia

V = potenciális energia

A hullámfüggvény előállításához ismernünk kell a Schrodinger-egyenletet, és az egyenletet kifejezzük

-đ^két/ 2μ * d^kétѱ_υ(Q) / dQ^két+ 1 / 2KQ^kétѱ_υ(Q) = E_υѱ_υ(Q) …………. egyenérték (2)

Ahol Q = a normál koordináta hossza

Μ = effektív tömeg

K = erőállandó

A Schrodinger-egyenlet határfeltételei:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Írhatjuk az (2) egyenletet is

d^kétѱ_υ(Q) / dQ^két+ 2μ / đ^két(E_υ-K / 2 * Q^két) ѱ_υ(Q) = 0 ………… egyenérték (3)

Az egyenlet megoldására használt paraméterek:

β = ђ / √μk ……… .. egyenérték (4)

d^két/ dQ^két= 1 / β^kétd^két/ dx^két………… .. egyenérték (5)

Helyettesítse az (4) és (5) egyenleteket az (3) egyenletben, ekkor az oszcillátor differenciálegyenlete

d^kétѱ_υ(Q) / dx^két+ (2μb^kétE_υ/ đ^két- x^két) ѱ_υ(x) = 0 ……… .. egyenérték (6)

A hatványsorok általános kifejezése az

ΣC¬nx2 …………. egyenérték (7)

Az exponenciális függvényt úgy fejezzük ki

exp (-x^két/ 2) ………… egyenérték (8)

eq (7) szorozva eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..eq (9)

A hermit polinomokat az alábbi egyenlet felhasználásával állíthatjuk elő

ђ_υ(x) = (-1)^υ* exp (x^két) d / dx^υ* exp (-x^két) …………… .. egyenérték (10)

A normalizáló állandót így fejezzük ki

N_υ= (1/2^υυ! √Π)^1/2…………… .eq (11)

A egyszerű harmonikus oszcillátor megoldás -ként fejezik ki

Ѱ_υ(x) = N_υH_υ(és) e^{-x2 / 2}……………… egyenérték (12)

Ahol N_υa normalizálási állandó

H _υa remete

van ^{-x2 / két}a Gauss-féle

A (12) egyenlet a harmonikus oszcillátor hullámfüggvénye.

Ez a táblázat a Hermite polinomok első kifejezését mutatja a legalacsonyabb energiaállapotokra

^υ	0	1	két	3
H_υ(Y)	1	2y	4y^két-két	8y³-12y

A hullámfüggvények egyszerű harmonikus oszcillátor gráf négy legalacsonyabb energiaállapot esetén az alábbi ábrák mutatják.

hullámfüggvények- harmonikus- oszcillátor

harmonikus oszcillátor hullámfüggvényei

Az oszcillátor valószínűségi sűrűségét a négy legalacsonyabb energiaállapotra az alábbi ábrák mutatják.

a hullámalakok valószínűsége -betegségei

hullámalakok valószínűség-sűrűsége

Alkalmazások

Az Simple harmonikus oszcillátoraz alkalmazások főleg a következőket tartalmazzák

Audio és Video rendszerek
Rádió és egyéb kommunikációs eszközök
Inverterek , Riasztások
Buzzerek
Dekoratív fények

Előnyök

A a harmonikus oszcillátor előnyei vannak

Olcsó
Nagyfrekvenciás generálás
Magas hatásfok
Olcsó
Hordozható
Gazdaságos

Példák

Ennek az oszcillátornak a példája a következőket tartalmazza.

Hangszerek
Egyszerű inga
Tömeges rugórendszer
Hinta
Az óra mutatóinak mozgása
Az autó, teherautó, buszok stb. Kerekeinek mozgása

Ez egyfajta mozgás, amelyet napi alapjainkon figyelhetünk meg. Harmonikus oszcillátor hullámfüggvény Schrodinger segítségével és levezetik a harmonikus oszcillátor egyenleteit. Itt egy kérdés, milyen típusú mozgást végez a bungee jumping?